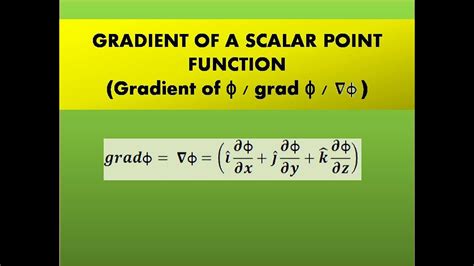
Gradient of a scalar point function
WebProperties and Applications Level sets. Where some functions have a given value, a level surface or isosurface is the set of all points. If the function f is differentiable, then at a point x the dot product of (∇ f) x . v of the gradient gives the directional derivative of function f at point x in the direction of v. To the level sets of f, the gradient of f is orthogonal. WebThe gradient of a scalar function f(x) with respect to a vector variable x = ( x1 , x2 , ..., xn ) is denoted by ∇ f where ∇ denotes the vector differential operator del. By definition, the gradient is a vector field whose components are the partial derivatives of f : The form of … The work done to compress the spring an additional 0.3 meters (i.e., moving the … List of Integrals Containing Exp - Gradient of a Scalar Function - Math . info Example:. Find the average value of the function f (x) = x 2 + 1 in the interval I = … For function f(x) such that f(x) and f′(x) are continuous on [a, b] .The length s of the … Infinite Series: Integral Test For Convergence The integral test for … In the above formula, n! denotes the factorial of n, and R n is a remainder … Using the cross product, determine the vector perpendicular to x 1 = (2, −3, 1) … Integrals Containing cos; Integrals Containing sin; Integrals Continaing sec; … Simple Functions; Logarithm and Exponential Functions; Trigonometric … Calculus includes the study of limits, derivatives, integrals, and infinite series.
Gradient of a scalar point function
Did you know?
WebApr 8, 2024 · The global convergence of the modified Dai–Liao conjugate gradient method has been proved on the set of uniformly convex functions. The efficiency and robustness of the newly presented methods are confirmed in comparison with similar methods, analyzing numerical results concerning the CPU time, a number of function evaluations, and the …
WebThe gradient of a multivariable function at a maximum point will be the zero vector, which corresponds to the graph having a flat tangent plane. Formally speaking, a local maximum point is a point in the input space such that all other inputs in a small region near that … http://www.math.info/Calculus/Gradient_Scalar/
WebNov 7, 2024 · In single variable scalar function $\ f(x)\ $ the sign of the derivative can tell you whether the function is increasing or decreasing at the point. I was trying to find an analogous concept in multi-variable scalar function $\varphi(\vec r)\ $ since its output is a scalar quantity just like in the single variable function. Now in these functions we have … WebJun 20, 2024 · The gradient of a scalar field is a vector field & is represented by vector point function whose magnitude is equal to the maximum rate of change of scalar point function in a direction in which …
The gradient (or gradient vector field) of a scalar function f(x1, x2, x3, …, xn) is denoted ∇f or ∇→f where ∇ (nabla) denotes the vector differential operator, del. The notation grad f is also commonly used to represent the gradient. The gradient of f is defined as the unique vector field whose dot product with any vector v at each point x is the directional derivative of f along v. That is, where the right-side hand is the directional derivative and there are many ways to represent it. F…
WebThe gradient of a scalar function (or field) is a vector-valued function directed toward the direction of fastest increase of the function and with a magnitude equal to the fastest … northman theWebVector Calculus: Understanding the Gradient. The gradient is a fancy word for derivative, or the rate of change of a function. It’s a vector (a direction to move) that. Points in the direction of greatest increase of a function ( intuition on why) Is zero at a local maximum or local minimum (because there is no single direction of increase ... northman thorirWebGravitational fields and electric fields associated with a static charge are examples of gradient fields. Recall that if f is a (scalar) function of x and y, then the gradient of f is. … how to scam on xboxWebTo calculate the gradient of a vector field in Cartesian coordinates, the following method is used : Given : S is a scalar field ( S is some function of x , y , and z) Find : grad S grad … how to scam online payday loansWebIf a vector field is the gradient of a scalar function then the curl of that vector field is zero. If the curl of some vector field is zero then that vector field is a the gradient of some scalar field. I have seen some trying to prove the first where I … how to scam on robloxWebIn this video you will understand aboutWhat is gradient of a scalar point function? and it's properties & example.Gradient of a scalar point function : https... how to scam people in factionsWebhow a scalar would vary as we moved off in an arbitrary direction. Here we find out how to. If is a scalar field, ie a scalar function of position in 3 dimensions, then its gradient at any point is defined in Cartesian co-ordinates by "$# ! It is usual to define the vector operator % " which is called “del” or “nabla”. northman titlovi